Trees 🌳🌴🌲
Introduction
A tree is a data structure that consists of nodes in a parent/child relationship. A tree can be empty with no nodes or a tree is made up of nodes where each node is a data structure consisting of a value, pointer to a parent node, and an array of children nodes. A tree data structure can represent information that naturally forms a hierarchy. For example, an organization chart is a tree structure.
Terminology
- Root - The top node in a tree.
- Child - A node directly connected to another node when moving away from the Root.
- Parent - The converse notion of a child.
- Siblings - A group of nodes with the same parent.
- Leaf - A node with no children.
- Edge - The connection between one node and another.
- Path - A sequence of nodes and edges connecting a node with a descendant.
- Level - Level of node is the number of edges on the path from the root node to the node.
- Height - Height of node is the number of edges on the longest path from the node to a leaf + 1.
- Depth - Depth of node is the number of edges from the node to the tree's root node.
Types of Trees
- General Tree - A tree data structure in which no node has a degree greater than two.
- Binary Tree - A tree data structure in which each node has a degree of zero,one or max two.
- Binary Search Tree - A binary tree in which the value of each node is greater than or equal to any value stored in the left sub-tree, and less than or equal to any value stored in the right sub-tree.
- Extended Binary Tree - A binary tree in which every node other than the leaves has two children.
- Complete Binary Tree - A binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Binary Tree
A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.
Properties of Binary Tree
- The maximum number of nodes at level ‘l’ of a binary tree is 2^l.
- Maximum number of nodes in a binary tree of height ‘h’ is 2^(h) – 1.
- In a Binary Tree with N nodes, minimum possible height or minimum number of levels is Log2(N+1)
- A Binary Tree with L leaves has at least Log2L + 1 levels
Binary Search Tree
A binary search tree is a binary tree in which the value of each node is greater than or equal to any value stored in the left sub-tree, and less than or equal to any value stored in the right sub-tree.
Properties of Binary Search Tree
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
- There must be no duplicate nodes.
- C Program
#include<stdio.h> #include<stdlib.h> struct node{ struct node*left; int data; struct node*right; }; struct node*root=NULL; void insert(int data) { struct node*newnode = (struct node*)malloc(sizeof(struct node)); newnode->data=data; newnode->left=NULL; newnode->right=NULL; if(root == NULL) { root = newnode; } else { struct node*temp = root; while(1) { if(data < temp->data) { if(temp->left == NULL) { temp->left = newnode; break; } else { temp = temp->left; } } else { if(temp->right == NULL) { temp->right = newnode; break; } else { temp = temp->right; } } } } } void search() { int key; printf("\nEnter element to search :"); scanf("%d",&key); struct node*temp = root; while(1) { if(key < temp->data) { if(temp->left == NULL) { printf("\nElement not found!"); break; } else if(temp->left->data == key) { printf("\nElement found"); return; } else { temp = temp->left; } } else { if(temp->right == NULL) { printf("\nElement not found!"); break; } else if(temp->right->data == key) { printf("\nElement found"); return; } else { temp = temp->right; } } } } int main() { int key,data,n; printf("\nEnter how many numbers you want to insert: "); scanf("%d",&n); for(int i=0;i<n;i++) { printf("\nEnter data : "); scanf("%d",&data); insert(data); } search(); } - Output
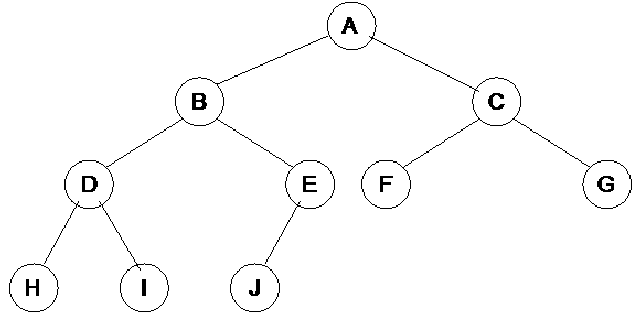
Complete Binary Tree
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Complete Binary tree looks like :
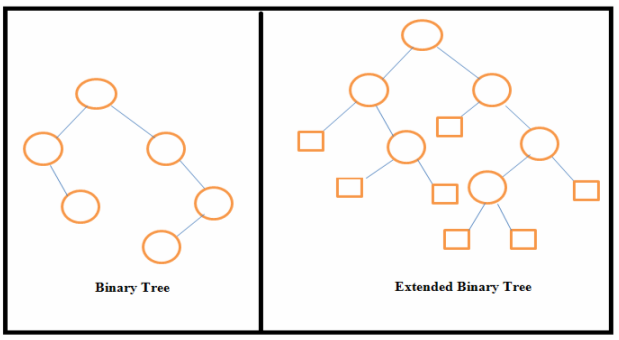
Extended Binary Tree
An extended binary tree is a binary tree in which every node other than the leaves has two children.
General tree can be converted to extended binary tree by adding dummy nodes.
Converting General tree to extended binary tree :
Representation of Binary trees in memory
1.Link
2.Sequential
Linked Representation
.

Chart form of above presentation
| Sr.No | left | Info | Right |
|---|---|---|---|
| 1 | -1 | K | -1 |
| 2 | 3 | E | -1 |
| 3 | -1 | Y | 4 |
| 4 | -1 | H | -1 |
| 5 | 1 | T | 6 |
| 6 | 8 | S | -1 |
| 7 | 2 | D | 5 |
| 8 | -1 | J | -1 |
| --- |
Sequential Representation
.
Rules :
- OneDirectional array called tree is used to store elements of tree.
-
The root of the tree will be at first index(instead of 0) i.e. tree[1] will store root node of tree
-
Children of node stored in location 2k (left node) and 2k+1 (right node).........(k = parent node)
-
Maximum size of array "tree" is given as 2^h - 1
-
An empty tree or subtree is specified by NULL i.e. tree[1]=NULL
Expression Tree 🌲⁎⁕/–🌲
Used for representing an equation
eg. 3+(5+9)*2

Traversing Binary Tree 🫱🏻🫲🏻
Preorder Traversal
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left-subtree)
- Traverse the right subtree, i.e., call Preorder(right-subtree)
Inorder Traversal
- Traverse the left subtree, i.e., call Inorder(left-subtree)
- Visit the root.
- Traverse the right subtree, i.e., call Inorder(right-subtree)
Postorder Traversal
- Traverse the left subtree, i.e., call Postorder(left-subtree)
- Traverse the right subtree, i.e., call Postorder(right-subtree)
- Visit the root.
#include <stdio.h>
#include <stdlib.h>
struct node
{
struct node* left;
int data;
struct node* right;
};
struct node*root=NULL;
void insert(int data)
{
struct node*newnode = (struct node*)malloc(sizeof(struct node));
newnode->data=data;
newnode->left=NULL;
newnode->right=NULL;
if(root == NULL)
{
root = newnode;
}
else
{
struct node*temp = root;
while(1)
{
if(data < temp->data)
{
if(temp->left == NULL)
{
temp->left = newnode;
break;
}
else
{
temp = temp->left;
}
}
else
{
if(temp->right == NULL)
{
temp->right = newnode;
break;
}
else
{
temp = temp->right;
}
}
}
}
}
void preorder(struct node* temp)
{
if(temp!=NULL)
{
printf("%d",&temp->data);
preorder(temp->left);
preorder(temp->right);
}
}
void inorder(struct node* temp)
{
if(temp!=NULL)
{
preorder(temp->left);
printf("%d",&temp->data);
preorder(temp->right);
}
}
void postorder(struct node* temp)
{
if(temp!=NULL)
{
preorder(temp->left);
preorder(temp->right);
printf("%d",&temp->data);
}
}
int main()
{
int n,data;
printf("Enter number of nodes :");
scanf("%d",&n);
for(int i=0;i<n;i++)
{
printf("\nEnter data : ");
scanf("%d",&data);
insert(data);
}
printf("\nPreoder : ");
preorder(root);
printf("\nInoder : ");
inorder(root);
printf("\nPostoder : ");
postorder(root);
return 0;
}
Enter number of nodes :8
Enter data : 6
Enter data : 1
Enter data : 7
Enter data : 0
Enter data : 2
Enter data : 8
Enter data : 5
Enter data : 9
Preoder : 6 1 0 2 5 7 8 9
Inoder : 1 0 2 5 6 7 8 9
Postoder : 1 0 2 5 7 8 9 6
BFS
Level Order Traversal
- Create an empty queue q
- temp_node = root /start from root/
- Loop while temp_node is not NULL a. print temp_node->data. b. Enqueue temp_node’s children (first left then right children) to q c. Dequeue a node from q and assign it’s value to temp_node
Spiral Order Traversal
- Create an empty queue q
- temp_node = root /start from root/
- Loop while temp_node is not NULL a. print temp_node->data. b. Enqueue temp_node’s children (first right then left children) to q c. Dequeue a node from q and assign it’s value to temp_node
Reverse Level Order Traversal
- Create an empty queue q
- temp_node = root /start from root/
- Loop while temp_node is not NULL a. print temp_node->data. b. Enqueue temp_node’s children (first right then left children) to q c. Dequeue a node from q and assign it’s value to temp_node
ZigZag Order Traversal
- Create an empty queue q
- temp_node = root /start from root/
- Loop while temp_node is not NULL a. print temp_node->data. b. Enqueue temp_node’s children (first right then left children) to q c. Dequeue a node from q and assign it’s value to temp_node
BFS Algorithm Applications
- To build index by search index
- For GPS navigation
- Path finding algorithms
- In Ford-Fulkerson algorithm to find maximum flow in a network
- Cycle detection in an undirected graph
- In minimum spanning tree
DFS
Inorder Traversal
- Create an empty stack S.
- Initialize current node as root
- Push the current node to S and set current = current->left until current is NULL
- If current is NULL and stack is not empty then a. Pop the top item from stack. b. Print the popped item, set current = popped_item->right c. Go to step 3.
- If current is NULL and stack is empty then we are done.
Preorder Traversal
- Create an empty stack S.
- Initialize current node as root
- Push the current node to S and set current = current->left until current is NULL
- If current is NULL and stack is not empty then a. Pop the top item from stack. b. Print the popped item, set current = popped_item->right c. Go to step 3.
- If current is NULL and stack is empty then we are done.
Postorder Traversal
- Create an empty stack S.
- Initialize current node as root
- Push the current node to S and set current = current->left until current is NULL
- If current is NULL and stack is not empty then a. Pop the top item from stack. b. Print the popped item, set current = popped_item->right c. Go to step 3.
- If current is NULL and stack is empty then we are done.
Application of DFS Algorithm
- For finding the path
- To test if the graph is bipartite
- For finding the strongly connected components of a graph
- For detecting cycles in a graph