Sorting techniques of arrays

Bubble sort

Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n2) where n is the number of items.

Pseudocode

procedure bubbleSort( A : list of sortable items )
    n = length(A)
    repeat
        swapped = false
        for i = 1 to n-1 inclusive do
            /* if this pair is out of order */
            if A[i-1] > A[i] then
                /* swap them and remember something changed */
                swap( A[i-1], A[i] )
                swapped = true
            end if
        end for
    until not swapped
end procedure

FLowchart

Bubble sort flowchart

CC++Python

#include <stdio.h>
int main()
{
    int arr[10], i, j, temp;
    printf("Enter the elements of the array: ");
    for (i = 0; i < 10; i++)
    {
        scanf("%d", &arr[i]);
    }
    for (i = 0; i < 10; i++)
    {
        for (j = i + 1; j < 10; j++)
        {
            if (arr[i] > arr[j])
            {
                temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
    }
    printf("The sorted array is: ");
    for (i = 0; i < 10; i++)
    {
        printf("%d ", arr[i]);
    }
    return 0;
}

#include <iostream>
using namespace std;
int main()
{
    int arr[10], i, j, temp;
    cout<<"Enter the elements of the array: ";
    for (i = 0; i < 10; i++)
    {
        cin>>arr[i];
    }
    for (i = 0; i < 10; i++)
    {
        for (j = i + 1; j < 10; j++)
        {
            if (arr[i] > arr[j])
            {
                temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
    }
    cout<<"The sorted array is: ";
    for (i = 0; i < 10; i++)
    {
        cout<<arr[i]<<" ";
    }
    return 0;
}

arr = []
print("Enter the elements of the array: ")
for i in range(10):
    arr.append(int(input()))
for i in range(10):
    for j in range(i + 1, 10):
        if arr[i] > arr[j]:
            temp = arr[i]
            arr[i] = arr[j]
            arr[j] = temp
print("The sorted array is: ")
for i in range(10):
    print(arr[i], end=" ")

Selection sort

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

Pseudocode

procedure selectionSort( A : list of sortable items )
    n = length(A)
    for i = 1 to n-1 inclusive do
        /* set current element as minimum*/
        min = i    
        /* check the element to be minimum */         
        for j = i+1 to n inclusive do
            if A[j] < A[min] then
                min = j;
            end if
        end for
        /* swap the minimum element with the current element*/  
        if indexMin != i  then
            swap A[min] and A[i]
        end if
    end for
end procedure

FLowchart

Selection sort flowchart

C

    #include <stdio.h>
    #include <stdlib.h>
        int main()
        {
            int *a, n, i, j, current, temp;
            printf("Enter number of elements :");
            scanf("%d", &n);

            a = (int *)malloc(n * sizeof(int));

            printf("Enter %d Numbers : ", n);
            for (i = 0; i < n; i++)
                scanf("%d", &a[i]);

            for(i = 0; i < n - 1; i++)
            {
                int min_idx= i;
                for(j = i + 1; j < n; j++)
                {
                    if(a[j] < a[min_idx])
                        temp = a[j];
                        a[j] = a[min_idx];
                        a[min_idx] = temp;
                }

            }
            printf("Sorted Array:n");
            for(i = 0; i < n; i++)
                printf("%dn", a[i]);
            return 0;
        }

C++

        #include <iostream>
        using namespace std;
        int main()
        {
            int a[100], n, i, j, position, swap;
            cout<<"Enter number of elementsn";
            cin>>n;
            cout<<"Enter "<<n<<" Numbersn";
            for (i = 0; i < n; i++)
                cin>>a[i];
            for(i = 0; i < n - 1; i++)
            {
                position=i;
                for(j = i + 1; j < n; j++)
                {
                    if(a[position] > a[j])
                    position=j;
                }
                if(position != i)
                {
                    swap=a[i];
                    a[i]=a[position];
                    a[position]=swap;
                }
            }
            cout<<"Sorted Array:n";
            for(i = 0; i < n; i++)
                cout<<a[i]<<"n";
            return 0;
        }

Insertion sort

Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.

Pseudocode

procedure insertionSort( A : list of sortable items )
    n = length(A)
    for i = 1 to n-1 inclusive do
        /* select value to be inserted */
        value = A[i]
        /* select hole position where number is to be inserted */
        hole = i
        /*locate hole position for the element to be inserted */
        while hole > 0 and A[hole-1] > value do
            A[hole] = A[hole-1]
            hole = hole -1
        end while
        /* insert the number at hole position */
        A[hole] = value
    end for
end procedure

Flowchart

Insertion sort flowchart

C

```c

include

int main(){ int *arr, i, j,size,current, temp; printf("Enter the size of the array: "); scanf("%d",&size);

    arr = (int*)malloc(size*sizeof(int));

    printf("Enter %d elements:",size);
    for (i = 0; i < size; i++)
    {
        scanf("%d", &arr[i]);
    }

    //logic
    for ( i = 0; i < size; i++)
    {
        current = arr[i];
        j=i-1;
        while(j>=0 && arr[j]>current)
        {
            arr[j+1]=arr[j];
            j--;
        }
        arr[j+1]=current;
    }

     printf("The sorted array is: ");
    for (i = 0; i < size; i++)
    {
        printf("%d ", arr[i]);
    }

return 0; } ```

C++

```c++

include

using namespace std;

int main(){ int *arr, i, j,size,current, temp; printf("Enter the size of the array: "); scanf("%d",&size);

arr = (int*)malloc(size*sizeof(int));

printf("Enter %d elements:",size);
for (i = 0; i < size; i++)
{
    cin>>arr[i];
}

//logic
for ( i = 1; i < size; i++)
{
    current = arr[i];
    j=i-1;
    while(j>=0 && arr[j]>current)
    {
        arr[j+1]=arr[j];
        j--;
    }
    arr[j+1]=current;
}

 printf("The sorted array is: ");
for (i = 0; i < size; i++)
{
    cout << arr[i]);
}

return 0; } ```

Radix sort

Radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys by the individual digits which share the same significant position and value. A positional notation is required, but because integers can represent strings of characters (e.g., names or dates) and specially formatted floating point numbers, radix sort is not limited to integers.

Pseudocode

procedure radixsort( list )
   bucket = new array of buckets
   for i = 0 to length(list) - 1
      insert list[i] into bucket[0]
   end for
   for i = 0 to 9
      sort bucket[i] using any sorting algorithm
      (recursive radix sort can be used here)
   end for
   concatenate the buckets
end procedure

Flowchart

Radix sort flowchart

CC++Python

#include<stdio.h>

int Getmax(int arr[],int size){
    int max=arr[0];
    for (int i = 1; i < size; i++)
    {
        if (arr[i]>max)
        {
            max=arr[i];
        }

    }
    return max;
}

void CountingSort(int arr[],int size,int div){
    int output[size];
    int count[10]={0};

    for (int i = 0; i < size; i++)
    {
        count[(arr[i]/div)%10]++;
    }
    for (int i = 1; i < 10; i++)
    {
        count[i]+=count[i-1];
    }
    for (int i = size-1; i >= 0; i--)
    {
        output[count[(arr[i]/div)%10 ]-1]=arr[i];
        count[(arr[i]/div)%10]--;
    }
    for (int i = 0; i < size; i++)
    {
        arr[i]=output[i];
    }

}

void radixSort(int arr[],int size){
    int m = Getmax(arr,size);

    for (int div= 1; m/div >0; div*=10)
    {
        CountingSort(arr,size,div);
    }

}

int main(){
int size;
printf("Enter size of array: )";
scanf("%d",&size);

int arr[size];
printf("Enter %d integers in any order : ",size);

for(int i=0;i<size;i++){
    scanf("%d",&arr[i]);
}

for(int i=0;i<size;i++){
    printf("%d ",arr[i]);
}

    printf("\n");
    radixSort(arr,size);

for(int i=0;i<size;i++){
    printf("%d",arr[i]);
}
    return 0;
}

#include<iostream>
using namespace std;

int Getmax(int arr[],int size){
    int max=arr[0];
    for (int i = 1; i < size; i++)
    {
        if (arr[i]>max)
        {
            max=arr[i];
        }

    }
    return max;
}

void CountingSort(int arr[],int size,int div){
    int output[size];
    int count[10]={0};

    for (int i = 0; i < size; i++)
    {
        count[(arr[i]/div)%10]++;
    }
    for (int i = 1; i < 10; i++)
    {
        count[i]+=count[i-1];
    }
    for (int i = size-1; i >= 0; i--)
    {
        output[count[(arr[i]/div)%10 ]-1]=arr[i];
        count[(arr[i]/div)%10]--;
    }
    for (int i = 0; i < size; i++)
    {
        arr[i]=output[i];
    }

}

void radixSort(int arr[],int size){
    int m = Getmax(arr,size);

    for (int div= 1; m/div >0; div*=10)
    {
        CountingSort(arr,size,div);
    }

}

int main(){
int size;
cout<<"Enter size of array: ";
cin>>size;

int arr[size];
cout<<"Enter "<<size<<" integers in any order : "<<endl;

for(int i=0;i<size;i++){
    cin >> arr[i];
}

for(int i=0;i<size;i++){
    cout<<arr[i]<<" ";
}

    cout<<endl;
    radixSort(arr,size);

for(int i=0;i<size;i++){
    cout<<arr[i]<<" ";
}
    return 0;
}

def Getmax(arr,size):
    max=arr[0]
    for i in range(1,size):
        if arr[i]>max:
            max=arr[i]
    return max

def CountingSort(arr,size,div):

    output=[0]*size
    count=[0]*10

    for i in range(0,size):
        count[(arr[i]/div)%10]+=1
    for i in range(1,10):
        count[i]+=count[i-1]
    for i in range(size-1,-1,-1):
        output[count[(arr[i]/div)%10]-1]=arr[i]
        count[(arr[i]/div)%10]-=1
    for i in range(0,size):
        arr[i]=output[i]

def radixSort(arr,size):
    m = Getmax(arr,size)

    div=1
    while m/div >0:
        CountingSort(arr,size,div)
        div*=10

size=int(input("Enter size of array: "))
arr=[]

print("Enter",size,"integers in any order : ")
for i in range(0,size):
    arr.append(int(input()))

print("Array before sorting: ")
for i in range(0,size):
    print(arr[i],end=" ")

radixSort(arr,size)

print("\nArray after sorting: ")
for i in range(0,size):
    print(arr[i],end=" ")

Merge Sort 🧩

Merge sort is a divide and conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one.

Pseudocode

```
mergeSort(arr[], l,  r)
If r > l
    1. Find the middle point to divide the array into two halves:  
        middle m = (l+r)/2
    2. Call mergeSort for first half:   
        Call mergeSort(arr, l, m)
    3. Call mergeSort for second half:
        Call mergeSort(arr, m+1, r)
    4. Merge the two halves sorted in step 2 and 3:
        Call merge(arr, l, m, r)
```

Algorithm

Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

Example

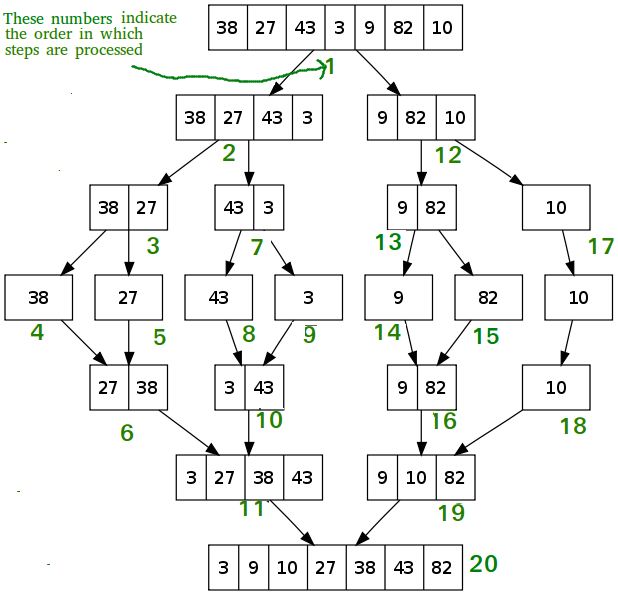
Merge Sort

Flowchart

Merge Sort Flowchart

Implementation

CC++Python

#include<stdio.h>
#include<stdlib.h>

void merge(int arr[],int l,int m,int r){
    int i,j,k;
    int n1=m-l+1;
    int n2=r-m;

    int L[n1],R[n2];

    for (i = 0; i < n1; i++)
    {
        L[i]=arr[l+i];
    }
    for (j = 0; j < n2; j++)
    {
        R[j]=arr[m+1+j];
    }
    i=0;
    j=0;
    k=l;

    while (i<n1 && j<n2)
    {
        if (L[i]<=R[j])
        {
            arr[k]=L[i];
            i++;
        }
        else
        {
            arr[k]=R[j];
            j++;
        }
        k++;
    }
    while (i<n1)
    {
        arr[k]=L[i];
        i++;
        k++;
    }
    while (j<n2)
    {
        arr[k]=R[j];
        j++;
        k++;
    }

}

void mergeSort(int arr[],int l,int r){
    if (l<r)
    {
        int m=l+(r-l)/2;

        mergeSort(arr,l,m);
        mergeSort(arr,m+1,r);

        merge(arr,l,m,r);
    }

}

void printArray(int arr[],int size){
    for (int i = 0; i < size; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
}

int main(){
    int arr[]={12,11,13,5,6,7};
    int size=sizeof(arr)/sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr,size);

    mergeSort(arr,0,size-1);

    printf("\nSorted array is \n");
    printArray(arr,size);
    return 0;
}

#include<iostream>
using namespace std;

void merge(int arr[],int l,int m,int r){
    int i,j,k;
    int n1=m-l+1;
    int n2=r-m;

    int L[n1],R[n2];

    for (i = 0; i < n1; i++)
    {
        L[i]=arr[l+i];
    }
    for (j = 0; j < n2; j++)
    {
        R[j]=arr[m+1+j];
    }
    i=0;
    j=0;
    k=l;

    while (i<n1 && j<n2)
    {
        if (L[i]<=R[j])
        {
            arr[k]=L[i];
            i++;
        }
        else
        {
            arr[k]=R[j];
            j++;
        }
        k++;
    }
    while (i<n1)
    {
        arr[k]=L[i];
        i++;
        k++;
    }
    while (j<n2)
    {
        arr[k]=R[j];
        j++;
        k++;
    }

}

void mergeSort(int arr[],int l,int r){
    if (l<r)
    {
        int m=l+(r-l)/2;

        mergeSort(arr,l,m);
        mergeSort(arr,m+1,r);

        merge(arr,l,m,r);
    }

}

void printArray(int arr[],int size){
    for (int i = 0; i < size; i++)
    {
        cout<<arr[i]<<" ";
    }
    cout<<endl;
}

int main(){
    int arr[]={12,11,13,5,6,7};
    int size=sizeof(arr)/sizeof(arr[0]);

    cout<<"Given array is \n";
    printArray(arr,size);

    mergeSort(arr,0,size-1);

    cout<<"\nSorted array is \n";
    printArray(arr,size);
    return 0;
}

def mergeSort(arr):
    if len(arr)>1:
        mid=len(arr)//2
        L=arr[:mid]
        R=arr[mid:]

        mergeSort(L)
        mergeSort(R)

        i=j=k=0

        while i<len(L) and j<len(R):
            if L[i]<R[j]:
                arr[k]=L[i]
                i+=1
            else:
                arr[k]=R[j]
                j+=1
            k+=1

        while i<len(L):
            arr[k]=L[i]
            i+=1
            k+=1

        while j<len(R):
            arr[k]=R[j]
            j+=1
            k+=1

def printList(arr):
    for i in range(len(arr)):
        print(arr[i],end=" ")
    print()

if __name__=="__main__":
    arr=[12,11,13,5,6,7]
    print("Given array is")
    printList(arr)
    mergeSort(arr)
    print("Sorted array is")
    printList(arr)

output

Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13

Time Complexity

The time complexity of merge sort is O(nlogn) in all the 3 cases (worst, average and best) as merge sort always divides the array into two halves and take linear time to merge two halves.

Space Complexity

The space complexity of merge sort is O(n) as we need to create a temporary array to store the elements while merging.

Applications

Merge Sort is useful for sorting linked lists in O(nLogn) time. In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked lists don’t have contiguous memory locations. Due to this difference, in arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in linked lists. Quick Sort requires a lot of this kind of access. In linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a continuous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low.

Shell Sort 🐚

Shell sort is mainly a variation of insertion sort. In insertion sort, we move elements only one position ahead. When an element has to be moved far ahead, many movements are involved. The idea of shell sort is to allow exchange of far items. In shell sort, we make the array h-sorted for a large value of h. We keep reducing the value of h until it becomes 1. An array is said to be h-sorted if all sublists of every h’th element is sorted.

Algorithm

Choose a value for h, called the increment. Start with large values of h and work down to a value of 1.
Divide the list into h sublists, where each sublist consists of all elements that are a distance h apart.
Sort each sublist using an insertion sort.
Repeat steps 2 and 3 until the list is sorted.

Flowchart

Shell Sort Flowchart

Implementation

CC++

#include<stdio.h>

void shellSort(int arr[],int n){
    for (int gap = n/2; gap > 0; gap/=2)
    {
        for (int i = gap; i < n; i++)
        {
            int temp=arr[i];
            int j=i;
            while(j >= gap && arr[j-gap]>temp)
            {
                arr[j]=arr[j-gap];
                j-=gap;
            }
            arr[j]=temp;
        }

    }

}

void printArray(int arr[],int n){
    for (int i = 0; i < n; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
}

int main(){
    int arr[]={12,34,54,2,3};
    int n=sizeof(arr)/sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr,n);

    shellSort(arr,n);

    printf("\nSorted array is \n");
    printArray(arr,n);
    return 0;
}

#include<iostream>
using namespace std;

void shellSort(int arr[],int n){
    for (int gap = n/2; gap > 0; gap/=2)
    {
        for (int i = gap; i < n; i++)
        {
            int temp=arr[i];
            int j;
            for (j = i; j >= gap && arr[j-gap]>temp; j-=gap)
            {
                arr[j]=arr[j-gap];
            }
            arr[j]=temp;
        }

    }

}

void printArray(int arr[],int n){
    for (int i = 0; i < n; i++)
    {
        cout<<arr[i]<<" ";
    }
    cout<<endl;
}

int main(){
    int arr[]={12,34,54,2,3};
    int n=sizeof(arr)/sizeof(arr[0]);

    cout<<"Given array is \n";
    printArray(arr,n);

    shellSort(arr,n);

    cout<<"\nSorted array is \n";
    printArray(arr,n);
    return 0;
}

Quick Sort

Quick sort is a divide and conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways.

Always pick first element as pivot.
Always pick last element as pivot (implemented below)
Pick a random element as pivot.
Pick median as pivot.

Algorithm

Pick an element, called a pivot, from the array.
Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.

Flowchart

Quick Sort Flowchart

Implementation

CC++Python

#include<stdio.h>

void swap(int *a,int *b){
    int temp=*a;
    *a=*b;
    *b=temp;
}

int partition(int arr[],int low,int high){
    int pivot=arr[high];
    int i=low-1;
    for (int j = low; j < high; j++)
    {
        if (arr[j]<pivot)
        {
            i++;
            swap(&arr[i],&arr[j]);
        }

    }
    swap(&arr[i+1],&arr[high]);
    return i+1;
}

void quickSort(int arr[],int low,int high){
    if (low<high)
    {
        int pi=partition(arr,low,high);
        quickSort(arr,low,pi-1);
        quickSort(arr,pi+1,high);
    }

}

void printArray(int arr[],int n){
    for (int i = 0; i < n; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
}

int main(){
    int arr[]={10,7,8,9,1,5};
    int n=sizeof(arr)/sizeof(arr[0]);

    quickSort(arr,0,n-1);
    printf("Sorted array: \n");
    printArray(arr,n);
    return 0;
}

    #include<iostream>
    using namespace std;

    void swap(int *a,int *b){
        int temp=*a;
        *a=*b;
        *b=temp;
    }

    int partition(int arr[],int low,int high){
        int pivot=arr[high];
        int i=low-1;
        for (int j = low; j < high; j++)
        {
            if (arr[j]<pivot)
            {
                i++;
                swap(&arr[i],&arr[j]);
            }

        }
        swap(&arr[i+1],&arr[high]);
        return i+1;
    }

    void quickSort(int arr[],int low,int high){
        if (low<high)
        {
            int pi=partition(arr,low,high);
            quickSort(arr,low,pi-1);
            quickSort(arr,pi+1,high);
        }

    }

    void printArray(int arr[],int n){
        for (int i = 0; i < n; i++)
        {
            cout<<arr[i]<<" ";
        }
        cout<<endl;
    }

    int main(){
        int arr[]={10,7,8,9,1,5};
        int n=sizeof(arr)/sizeof(arr[0]);

        quickSort(arr,0,n-1);
        cout<<"Sorted array: \n";
        printArray(arr,n);
        return 0;
    }

    def partition(arr,low,high):
        i=low-1
        pivot=arr[high]
        for j in range(low,high):
            if arr[j]<pivot:
                i+=1
                arr[i],arr[j]=arr[j],arr[i]
        arr[i+1],arr[high]=arr[high],arr[i+1]
        return i+1

    def quickSort(arr,low,high):
        if low<high:
            pi=partition(arr,low,high)
            quickSort(arr,low,pi-1)
            quickSort(arr,pi+1,high)

    def printArray(arr):
        for i in range(len(arr)):
            print(arr[i],end=" ")
        print()

    if __name__=="__main__":

        arr=[10,7,8,9,1,5]
        n=len(arr)

        quickSort(arr,0,n-1)
        print("Sorted array: ")
        printArray(arr)

Time Complexity

Worst Case Time Complexity [ Big-O ]: O(n^2)
Best Case Time Complexity [Big-omega]: O(n*log n)
Average Time Complexity [Big-theta]: O(n*log n)
Space Complexity: O(n)

Applications

Quick Sort is used in many real life applications like in sorting a deck of cards, sorting files on a disk, sorting names in a phone book, sorting student records etc.

Cocktail Sort 🍷

Cocktail Sort is a variation of Bubble sort. The Bubble sort algorithm always traverses elements from left and moves the largest element to its correct position in first iteration and second largest in second iteration and so on. Cocktail Sort traverses through a given array in both directions alternatively.

Algorithm

Initially, we start the loop from left side and move the largest element to the end of the array.
Then, we start the loop from right side and move the smallest element to the beginning of the array.
This process goes on until the array is sorted.

Flowchart

Cocktail Sort Flowchart

Implementation

CC++

#include<stdio.h>

void cocktailSort(int arr[],int n){
    int swapped=1;
    int start=0;
    int end=n-1;

    while (swapped)
    {
        swapped=0;

        for (int i = start; i < end; i++)
        {
            if (arr[i]>arr[i+1])
            {
                int temp=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=temp;
                swapped=1;
            }
        }

        if (!swapped)
        {
            break;
        }
        swapped=0;
        end--;

        for (int i = end-1; i >= start; i--)
        {
            if (arr[i]>arr[i+1])
            {
                int temp=arr[i];
                arr[i]=arr[i+1];
                arr[i+1]=temp;
                swapped=1;
            }
        }
        start++;
    }
}

void printArray(int arr[],int n){
    for (int i = 0; i < n; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
}

int main(){
    int arr[]={5,1,4,2,8,0,2};
    int n=sizeof(arr)/sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr,n);

    cocktailSort(arr,n);

    printf("\nSorted array is \n");
    printArray(arr,n);
    return 0;
}

    #include<bits/stdc++.h>
    using namespace std;

    // Sorts array a[0..n-1] using Cocktail sort
    void CocktailSort(int a[], int n)
    {
    bool swapped = true;
    int start = 0;
    int end = n - 1;

    while (swapped) {
    // reset the swapped flag on entering
    // the loop, because it might be true from
    // a previous iteration.
    swapped = false;

    // loop from left to right same as
    // the bubble sort
    for (int i = start; i < end; ++i) {
    if (a[i] > a[i + 1]) {
        swap(a[i], a[i + 1]);
        swapped = true;
    }
    }

    // if nothing moved, then array is sorted.
    if (!swapped)
    break;

    // otherwise, reset the swapped flag so that it
    // can be used in the next stage
    swapped = false;

    // move the end point back by one, because
    // item at the end is in its rightful spot
    --end;

    // from right to left, doing the
    // same comparison as in the previous stage
    for (int i = end - 1; i >= start; --i) {
    if (a[i] > a[i + 1]) {
        swap(a[i], a[i + 1]);
        swapped = true;
    }
    }

    // increase the starting point, because
    // the last stage would have moved the next
    // smallest number to its rightful spot.
    ++start;
    }
    }

    /* Prints the array */
    void printArray(int a[], int n)
    {
    for (int i = 0; i < n; i++)
    printf("%d ", a[i]);
    printf("\n");
    }

    // Driver code
    int main()
    {
    int arr[] = { 5, 1, 4, 2, 8, 0, 2 };
    int n = sizeof(arr) / sizeof(arr[0]);
    CocktailSort(arr, n);
    printf("Sorted array :\n");
    printArray(arr, n);
    return 0;
    }

output

    Given array is
    5 1 4 2 8 0 2

    Sorted array is
    0 1 2 2 4 5 8

Time Complexity

The time complexity of Cocktail Sort is O(n2) in worst case and O(n) in best case.

Space Complexity

The space complexity of Cocktail Sort is O(1) as it is an in-place sorting algorithm.

Applications

Cocktail Sort is useful when the array is reverse sorted.
Cocktail Sort is also useful when the array is sorted in ascending order and few elements are misplaced in the array.

Sorting techniques of arrays

Bubble sort

Pseudocode

FLowchart

Selection sort

Pseudocode

FLowchart

Insertion sort

Pseudocode

Flowchart

include

include

include

Radix sort

Pseudocode

Flowchart

Merge Sort 🧩

Pseudocode

Algorithm

Example

Flowchart

Implementation

**Time Complexity **

**Space Complexity **

**Applications **

Shell Sort 🐚

**Algorithm **

Flowchart

**Implementation **

Quick Sort

**Algorithm **

Flowchart

**Implementation **

**Time Complexity **

**Applications **

**Cocktail Sort 🍷 **

**Algorithm **

Flowchart

**Implementation **

**Time Complexity **

**Space Complexity **

**Applications **

Time Complexity

Space Complexity

Applications

Algorithm

Implementation

Algorithm

Implementation

Time Complexity

Applications

Cocktail Sort 🍷

Algorithm

Implementation

Time Complexity

Space Complexity

Applications